第三種電気主任技術者試験過去問 機械科目 令和元年度
オプション
問題文正答率:33.33%
問1 直流電源に接続された永久磁石界磁の直流電動機に一定トルクの負荷がつながっている。電機子抵抗が1.00Ωである。回転速度が1000 min\(^{-1}\)のとき,電源電圧は120V,電流は20 Aであった。
この電源電圧を100Vに変化させたときの回転速度の値[min\(^{-1}\)]として,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,電機子反作用及びブラシ,整流子における電圧降下は無視できるものとする。
https://ja.mondder.com/fq?id=1764🔗
問題文正答率:33.33%
問2 直流機の電機子反作用に関する記述として,誤っているものを次の(1)~(5) のうちから一つ選べ。
解説・コメント
(1)正
(2)誤。電機子電流による起電力は、界磁磁束の向きと直行するため、「同じ向き」としている箇所が誤り。
(3)正
(4)正
(5)正
https://ja.mondder.com/fq?id=1765🔗
問題文正答率:33.33%
問3 4極の三相誘導電動機が60Hzの電源に接続され,出力5.75kW,回転速度 1656min\(^{-1}\)で運転されている。このとき,一次銅損,二次銅損及び鉄損の三つの損失の値が等しかった。このときの誘導電動機の効率の値[%]として,最も近い ものを次の(1)~(5)のうちから一つ選べ。
ただし,その他の損失は無視できるものとする。
解説・コメント
同期速度N\(_s\)は、
N\(_s\)=120×f/p=1800min\(^{-1}\)
回転速度は問題文より、1656min\(^{-1}\)なので、すべりsは
s=(1800-1656)/1800=0.08
出力をP\(_0\)とすると、二次銅損P\(_c2\)は、
P\(_c2\)=P\(_0\)×s/(1-s)=5.75×0.08/(1-0.08)=0.5[kW]全損失は一次銅損と二次銅損と鉄損の合計であるため、題意より、
0.5+0.5+0.5=1.5[kW]効率は5.75/(5.75+1.5)≒0.793 → 79.3%
https://ja.mondder.com/fq?id=1766🔗
問題文正答率:33.33%
問4 次の文章は,誘導機の速度制御に関する記述である。
誘導機の回転速度n [min\(^{-1}\)]は,滑りs,電源周波数f[Hz],極数pを用いてn = 120• (ア) と表される。したがって,誘導機の速度は電源周波数によって制御することができ,特にかご形誘導電動機において (イ) 電源装置を用いた制御が広く利用されている。
かご形誘導機ではこの他に,運転中に固定子巻線の接続を変更して (ウ) を切り換える制御法や, (エ) の大きさを変更する制御法がある。前者は,効率はよいが,速度の変化が段階的となる。後者は,速度の安定な制御範囲を広くするために (オ) の値を大きくとり,銅損が大きくなる。
巻線形誘導機では, (オ) の値を調整することにより,トルクの比例推移を利用して速度を変える制御法がある。
上記の記述中の空白箇所(ア),(イ),(ウ),(エ)及び(オ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
解説・コメント
回転速度n [min\(^{-1}\)]は,滑りs,電源周波数f[Hz],極数pを用いてn = 120•(1-s)f/pと表される。
かご形誘導電動機の速度制御で広く利用されるVVVF(可変電圧可変周波数)電源制御を用いることが多い。
かご形誘導電動機では、運転中に固定子巻線の接続を変更して極数を切り替える制御法や、一次電圧の大きさを変更する制御法がある。
一次電圧の大きさを変更する制御法は、速度の安定な制御範囲を広くするために二次抵抗の値を大きくとり、銅損が大きくなる。
巻線形誘導機では、二次抵抗の値を調整することにより、トルクの比例推移を利用して速度を変える制御法がある。
https://ja.mondder.com/fq?id=1767🔗
問題文正答率:33.33%
問5 次の文章は,星形結線の円筒形三相同期電動機の入力,出力,トルクに関する記述である。
この三相同期電動機の1相分の誘導起電力E[V],電圧V[V],電流I[A],VとIの位相差をθ[rad]としたときの1相分の入力P\(_i\) [W]は次式で表される。
P\(_i\)=VITcosθ
また,EとVの位相差をδ[rad]とすると,1相分の出力P\(_o\)[W]は次式で表される。EとVの位相差δは (ア) といわれる。
P\(_o\)=EIcos(δ-θ)=\(\frac{VE}{x}\) (イ)ここでx[Ω]は同期リアクタンスであり,電機子巻線抵抗は無視できるものとする。
この三相同期電動機の全出力をP[W],同期速度をn\(_s\)[min\(^{-1}\)]とすると,トルク T[N•m]とPの関係は次式で表される。
P = 3P\(_o\)=2π\(\frac{n_s}{60}\)T
これから,Tは次式のようになる。
T=\(\frac{60}{2πn_s}・3P_o=\frac{60}{2πn_s}・\frac{3VE}{x}\) (イ)以上のことから, 0≦δ≦\(\frac{π}{2}\)の範囲においてδが (ウ) なるに従ってTは (エ) なり,理論上\(\frac{π}{2}\)[rad]のとき (オ) となる。
上記の記述中の空白箇所(ア),(イ),(ウ),(エ)及び(オ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
解説・コメント
EとVの位相差をδ[rad]とすると,1相分の出力P\(_o\)[W]は次式で表される。EとVの位相差δは 負荷角といわれる。
P\(_o\)=EIcos(δ-θ)=\(\frac{VE}{x}\)sinδ
T=\(\frac{60}{2πn_s}・3P_o=\frac{60}{2πn_s}・\frac{3VE}{x}\)sinδ
0≦δ≦\(\frac{π}{2}\)の範囲においてδが大きくなるに従ってTは大きくなり,理論上\(\frac{π}{2}\)[rad]のとき最大値となる。
https://ja.mondder.com/fq?id=1768🔗
問題文正答率:33.33%
問6 次の文章は,一般的なブラシレスDCモータに関する記述である。
ブラシレスDCモータは, (ア) が回転子側に, (イ) が固定子側に取り付けられた構造となっており, (イ) が回転しないため, (ウ) が必要な一般の直流電動機と異なる。しかし,何らかの方法で回転子の (エ) を検出して, (イ) への電流を切り換える必要がある。この電流の切り換えを, (オ) で構成された駆動回路を用いて実現している。ブラシレスDCモータは, (オ) の発達とともに発展してきたモータであり,上記の駆動回路が重要な役割を果たすモータである。
上記の記述中の空白箇所(ア),(イ),(ウ),(エ)及び(オ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
解説・コメント
ブラシレスDCモータの回転子は永久磁石であり、固定子には三相巻線を施した磁極がある。
ブラシレスDCモータは, 永久磁石 が回転子側に,電機子巻線が固定子側に取り付けられた構造となっており,電機子巻線が回転しないため, ブラシと整流子が必要な一般の直流電動機と異なる。しかし,何らかの方法で回転子の回転位置を検出して, 電機子巻線への電流を切り換える必要がある。この電流の切り換えを,半導体スイッチで構成された駆動回路を用いて実現している。ブラシレスDCモータは, 半導体スイッチの発達とともに発展してきたモータであり,上記の駆動回路が重要な役割を果たすモータである。
https://ja.mondder.com/fq?id=1769🔗
問題文正答率:33.33%
問7 次の文章は,電気機器の損失に関する記述である。
a コイルの電流とコイルの抵抗によるジュール熱が (ア) であり,この損失 を低減するため,コイルを構成する電線の断面積を大きくする。
交流電流が並列コイルに分かれて流れると,並列コイル間の電流不平衡からこの損失が増加する。この損失を低減するため,並列回路を構成する各コイルの鎖交磁束と抵抗値,すなわち,各コイルのインピーダンスを等しくする。
b 鉄心に交流磁束が通ると損失が発生する。その成分は (イ) と (ウ) の二つに分類される。前者は,交流磁束によって誘導された電流が鉄心を流れてジュール熱として発生する。そこで,電気抵抗が高い強磁性材料や,表面を絶縁膜で覆った薄い鉄板を積層した積層鉄心を磁気回路に用いて,電流の経路を断つことで損失を低減する。後者は,鉄心の磁束が磁界の履歴に依存するた めに発生する。この (ウ) を低減するために電磁鋼板が磁気回路に広く用い られている。
c 上記の電磁気要因の損失のほか,電動機や発電機では,回転子の運動による軸受け摩擦損や冷却ファンの空気抵抗による損失などの (エ) がある。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
解説・コメント
鉄損や機械損は、機器に負荷をかけなくてもほぼ一定の大きさで存在するため、これを無負荷損または固定損という。一方、負荷電流によって変化する銅損を負荷損という。
また、機械損のうち、空気抵抗によるものを風損という。
a コイルの電流とコイルの抵抗によるジュール熱が銅損であり,この損失 を低減するため,コイルを構成する電線の断面積を大きくする。
b 鉄心に交流磁束が通ると損失が発生する。その成分は渦連流損 と ヒステリシス損の二つに分類される。前者は,交流磁束によって誘導された電流が鉄心を流れてジュール熱として発生する。そこで,電気抵抗が高い強磁性材料や,表面を絶縁膜で覆った薄い鉄板を積層した積層鉄心を磁気回路に用いて,電流の経路を断つことで損失を低減する。後者は,鉄心の磁束が磁界の履歴に依存するた めに発生する。このヒステリシス損を低減するために電磁鋼板が磁気回路に広く用い られている。
c 上記の電磁気要因の損失のほか,電動機や発電機では,回転子の運動による軸受け摩擦損や冷却ファンの空気抵抗による損失などの 機械損がある。
https://ja.mondder.com/fq?id=1770🔗
問題文正答率:33.33%
問8 2台の単相変圧器があり,それぞれ,巻数比(一次巻数/二次巻数)が30.1, 30.0,二次側に換算した巻線抵抗及び漏れリアクタンスからなるインピーダンスが(0.013+j0.022) Ω, (0.010+j0.020) Ωである。この2台の変圧器を並列接続し二次側を無負荷として,一次側に6600Vを加えた。この2台の変圧器の二次巻線間を循環して流れる電流の値[A]として,最も近いものを次の(1)~(5)のうちから一つ選べ。ただし,励磁回路のアドミタンスの影響は無視するものとする。
解説・コメント
二次側には、一次側の2つの電源の起電力差によって電流が流れる。
起電力差V=6600/30 - 6600/30.1 ≒0.7309
二次側の合成インピーダンスは
(0.0013+j0.022)+ (0.01+j0.020) =0.023+j0.042
電流の大きさは
0.7309/(0.023\(^{2}\)+0.042\(^{2}\))\(^{1/2}\) ≒ 15.3[A]https://ja.mondder.com/fq?id=1771🔗
問題文正答率:33.33%
問9 変圧器の試験方法の一つに温度上昇試験がある。小形変圧器の場合には実負荷法を用いるが,電力用等の大形変圧器では返還負荷法を用いる。返還負荷法では,外部電源から鉄損と銅損に相当する電力のみを供給すればよいので試験電源が比較的小規模なものですむ。単相変圧器におけるこの試験の結線方法及び図中に示す鉄損,銅損の供給方法として,次の(1) ~(5) のうちから正しいものを一つ選べ。ただし,T\(_1\),T\(_2\)は試験対象となる同じ仕様の変圧器,T\(_3\)は補助変圧器である。
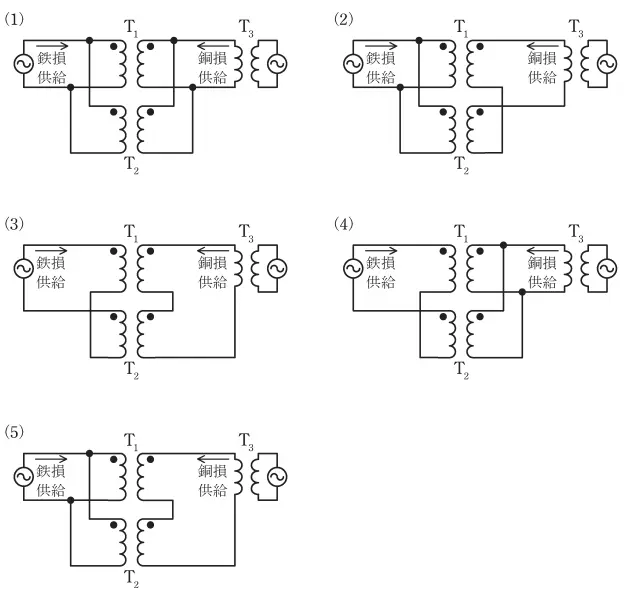
解説・コメント
一般的に、返還負荷法では、低圧側から鉄損を供給し、高圧側から銅損を供給する。
鉄損を供給する側では、端子の極数が同じ向きになるように並列に接続し、同じ定格電圧を加える。
銅損を供給する側では、2台の変圧器の極性を起電力を打ち消す向きに直列に接続する。
https://ja.mondder.com/fq?id=1772🔗
問題文正答率:33.33%
問10 次の文章は,単相サイリスタ整流回路に関する記述である。
図1には純抵抗負荷に接続された単相サイリスタ整流回路を示し,T\(_1\)~T\(_4\)のサ イリスタはオン電圧降下を無視できるものとする。また,図1中の矢印の方向を正とした交流電源の電圧\(v\) = Vsin\(wt\)[V]及び直流側電圧\(v_d\)の波形をそれぞれ破線及び実線で図2に示す。
図2に示した交流電圧の位相において,π<\(wt\)<2πの位相で同時にオン信号を与えるサイリスタは (ア) である。
交流電圧1サイクルの中で,例えばサイリスタT\(_4\)からT\(_2\)へ導通するサイリスタが換わる動作を考える。T\(_4\)がオンしている状態から位相πで電流が零になると,T\(_4\)はオフ状態となる。その後,制御遅れ角αを経てT\(_2\)にオン信号を与えると,電流がT\(_2\)に流れる。このとき既に電流が零になったT\(_4\)には,交流電圧\(v\)が (イ) として印加される。すなわち, (ウ) であるサイリスタは,極性が変わる交流電圧を利用してターンオフすることができる。
次に交流電圧と直流側電圧の関係について考える。サイリスタT\(_2\)とT\(_3\)がオンしている期間は交流電源の (エ) と直流回路のN母線が同じ電位になるので,このときの直流側電圧\(v_d\)は (オ) と等しくなる。
上記の記述中の空白箇所(ア),(イ),(ウ),(エ)及び(オ)に当てはまる組合せとして, 正しいものを次の(1)~(5)のうちから一つ選べ。
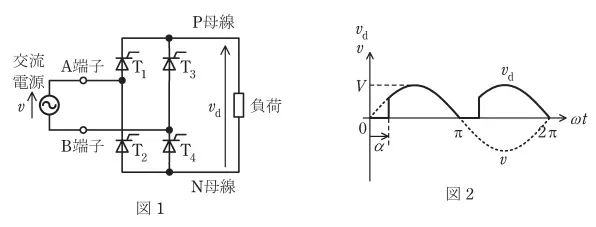
解説・コメント
サイリスタブリッジの基本構成である。サイリスタは自己消弧形素子ではないので、ゲート信号でターンオンできるが自力でターンオフはできないため、電源電圧を利用してターンオフさせる。
π<\(wt\)<2πの位相で同時にオン信号を与えるサイリスタはT\(_2\) と T\(_3\)である。
交流電圧1サイクルの中で,例えばサイリスタT\(_4\)からT\(_2\)へ導通するサイリスタが換わる動作を考える。T\(_4\)がオンしている状態から位相πで電流が零になると,T\(_4\)はオフ状態となる。その後,制御遅れ角αを経てT\(_2\)にオン信号を与えると,電流がT\(_2\)に流れる。このとき既に電流が零になったT\(_4\)には,交流電圧\(v\)が 逆電圧として印加される。すなわち, オン制御デバイスであるサイリスタは,極性が変わる交流電圧を利用してターンオフすることができる。
次に交流電圧と直流側電圧の関係について考える。サイリスタT\(_2\)とT\(_3\)がオンしている期間は交流電源のA端子と直流回路のN母線が同じ電位になるので,このときの直流側電圧\(v_d\)は交流電圧の逆方向電圧-\(v\)と等しくなる。
https://ja.mondder.com/fq?id=1773🔗
問題文正答率:33.33%
問11 かごの質量が250kg,定格積載質量が1500 kgのロープ式エレベータにおいて,釣合いおもりの質量は,かごの質量に定格積載質量の50%を加えた値とした。このエレベータの電動機出力を22kWとした場合,一定速度でかごが上昇しているときの速度の値[m/min]はいくらになるか,最も近いものを次の(1)~(5) のうちから一つ選べ。ただし,エレベータの機械効率は70 %,積載量は定格積載質量とし,ロープの質量は無視するものとする。
解説・コメント
電動機の巻き上荷重Mは、かごの質量と積載質量の合計から、釣合いおもりの質量を引いたものとなる。
釣合いおもりの質量は問題文より、250+0.5×1500=1000[kg]M=250+1500-1000=750[kg]エレベータ機械効率が0.7であり、巻き上げ速度をV[m/min]とすると、
22×10\(^{3}\)/0.7 = 9.8×750×V/60
V≒126[m/min]https://ja.mondder.com/fq?id=1774🔗
問題文正答率:33.33%
問12 次の文章は,太陽光発電システムに関する記述である。
太陽光発電システムは,太陽電池アレイ,パワーコンディショナ,これらを接続する接続箱,交流側に設置する交流開閉器などで構成される。太陽電池アレイは,複数の太陽電池 (ア) を通常は直列に接続して構成される太陽電池 (イ) をさらに直並列に接続したものである。パワーコンディショナは,直流を交流に変換する (ウ) と,連系保護機能を実現する系統連系用保護装置などで構成されている。
太陽電池アレイの出力は,日射強度や太陽電池の温度によって変動する。これらの変動に対し,太陽電池アレイから常に (エ) の電力を取り出す制御は, MPPT (Maximum Power Point Tracking)制御と呼ばれている。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
解説・コメント
MPPT制御は、最大電力を取り出せるような動作点で動作するように制御する方法である。
太陽光発電システムは,太陽電池アレイ,パワーコンディショナ,これらを接続する接続箱,交流側に設置する交流開閉器などで構成される。太陽電池アレイは,複数の太陽電池セルを通常は直列に接続して構成される太陽電池モジュールをさらに直並列に接続したものである。パワーコンディショナは,直流を交流に変換するインバータと,連系保護機能を実現する系統連系用保護装置などで構成されている。
太陽電池アレイの出力は,日射強度や太陽電池の温度によって変動する。これらの変動に対し,太陽電池アレイから常に最大の電力を取り出す制御は, MPPT (Maximum Power Point Tracking)制御と呼ばれている。
https://ja.mondder.com/fq?id=1775🔗
問題文正答率:33.33%
問13 図1に示すR-L回路において,端子a-a’間に5Vの階段状のステップ電圧 \(v_1(t)\) [V]を加えたとき,抵抗\(R_2\)[Ω]に発生する電圧を\(v_2(t)\) [V]とすると,\(v_2(t)\)は図2のようになった。この回路の\(R_1\)[Ω],\(R_2\)[Ω]及びL[H]の値と,入力を\(v_1(t)\),出力を\(v_2(t)\)としたときの周波数伝達関数G(jω)の式として,正しいものを次の(1)~(5) のうちから一つ選べ。
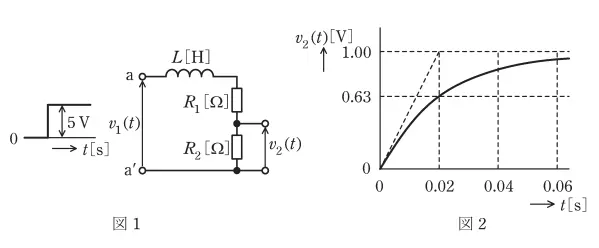
解説・コメント
図2より、時定数τが0.02であることが読み取れる。
τ=L/((\(R_1\)+\(R_2\))=0.02
これを満たす組み合わせは(2)と(4)
十分時間が経過した定常状態ではLの起電力はゼロであり、その時の電圧\(v_2(t)\)は図2より1Vであることから、
(\(R_1\):\(R_2\) = 4:1
ここで\(v_1\)と\(v_2\)をjωの関数に置き換えると、
\(V_2(jω)\)=\(R_2\)×\(V_1(jω)\)/( (\(R_1\)+\(R_2\)) + jωL)となるので、G(jω)は\(V_2(jω)\)/\(V_1(jω)\)=\(R_2\)/( (\(R_1\)+\(R_2\)) + jωL)
\(R_2\)/( (\(R_1\)+\(R_2\))=0.2、L/( (\(R_1\)+\(R_2\))=0.02よりG(jω)=\(\frac{0.2}{1 + j0.02ω}\)
https://ja.mondder.com/fq?id=1776🔗
問題文正答率:33.33%
問14 2進数AとBがある。それらの和がA+B=(101010)\(_2\),差がA-B=(1100)\(_2\)であるとき,Bの値として,正しいものを次の(1)~(5)のうちから一つ選べ。
解説・コメント
2進数を10進数に変換して考える。
A+B=42
A-B=12
この連立方程式から、B=15
15を2進数で表すと、(1111)\(_2\) となる。
https://ja.mondder.com/fq?id=1777🔗
問題文正答率:33.33%
問15 並行運転しているA及びBの2台の三相同期発電機がある。それぞれの発電機の負荷分担が同じ7300kWであり,端子電圧が6600Vのとき,三相同期発電機Aの負荷電流\(I_A\)が1000 A ,三相同期発電機Bの負荷電流\(I_B\)が800 Aであった。損失は無視できるものとして,次の(a)及び(b)の問に答えよ。
(a)三相同期発電機Aの力率の値[%]として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(b) 2台の発電機の合計の負荷が調整の前後で変わらずに一定に保たれているものとして,この状態から三相同期発電機A及びBの励磁及び駆動機の出力を調整し,三相同期発電機Aの負荷電流は調整前と同じ1000 Aとし,力率は 100%とした。このときの三相同期発電機Bの力率の値[%]として,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,端子電圧は変わらないものとする。
解説・コメント
(a)
発電機Aの力率をcosθとすると、
3\(^{1/2}\)×6600×1000×cosθ=7300×10\(^{3}\)
cosθ≒0.639 → 64%
(b)
負荷の有効電力および無効電力の合計が調整前後で変わっていないことを利用する。
有効電力は発電機A,B共に7300[kW]発電機Aの無効電力は3\(^{1/2}\)×6600×1000×sinθ≒8793[kvar]発電機BもAと同様にまずはconθを計算する。
3\(^{1/2}\)×6600×800×cosθ=7300×10\(^{3}\)
cosθ≒0.798
無効電力は3\(^{1/2}\)×6600×800×sinθ≒5511[kvar]次に調整後の計算を行う。
発電機Aの力率が100%であることからcosθ=1
有効電力は3\(^{1/2}\)×6600×1000×cosθ≒11432[kW]無効電力は0
有効電力の合計は7300×2なので、
発電機Bで賄う有効電力は7300×2-11432≒3168[kW]同じ要領で無効電力は8793+5511-0=14304[kvar]これより、発電機Bの皮相電力は(3168\(^{2}\)+14304\(^{2}\))\(^{1/2}\)≒14651[kVA]発電機Bの力率cosθ=3168/14651≒0.216 → 22%
https://ja.mondder.com/fq?id=1778🔗
問題文正答率:33.33%
問16 図は直流昇圧チョッパ回路であり,スイッチングの周期をT[s]とし,その中での動作を考える。ただし,直流電源Eの電圧をE\(_0\)[V]とし,コンデンサCの容量は十分に大きく出力電圧E\(_1\)[V]は一定とみなせるものとする。
半導体スイッチSがオンの期間T\(_{on}\)[s]では,EーリアクトルL-S-Eの経路とC-負荷R-Cの経路の二つで電流が流れ,このときにLに蓄えられるエネルギーが増加する。Sがオフの期間T\(_{off}\)[s]では,E-L-ダイオードD-(CとRの並列回路)-Eの経路で電流が流れ,Lに蓄えられたエネルギーが出力側に放出される。次の(a)及び(b)の問に答えよ。
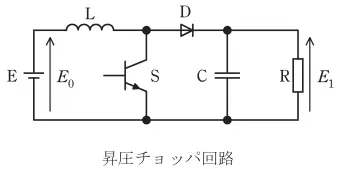
(a)この動作において,Lの磁束を増加させる電圧時間積は (ア) であり,磁束を減少させる電圧時間積は (イ) である。定常状態では,増加する磁束と 減少する磁束が等しいとおけるので,入力電圧と出力電圧の関係を求めることができる。
上記の記述中の空白箇所(ア)及び(イ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
(b)入力電圧\(E_0\)=100 V,通流率α = 0.2のときに,出力電圧\(E_1\)の値[V]として, 最も近いものを次の(1)~(5)のうちから一つ選べ。
解説・コメント
(a)
問題文に「半導体スイッチSがオンの期間T\(_{on}\)[s]では,EーリアクトルL-S-Eの経路とC-負荷R-Cの経路の二つで電流が流れ,このときにLに蓄えられるエネルギーが増加する。」とあるため、Lの磁束を増加させる時間はT\(_{on}\)[s]であることがわかる。
T\(_{off}\)[s]で磁束を減少させることになるが、Lには電位差E\(_{1}\)-E\(_{0}\)が加わる。
(b)
昇圧チョッパの公式E\(_{1}\)=E\(_{0}\)/(1-α)=125[V]https://ja.mondder.com/fq?id=1779🔗
問題文正答率:33.33%
問17 電気給湯器を用いて,貯湯タンクに入っている温度20℃,体積0.37m\(^3\)の水を85℃に加熱したい。水の比熱容量は4.18x10\(^3\) j/(kg・K),水の密度は1.00x10\(^3\) kg/m\(^3\)であり,いずれも水の温度に関係なく一定とする。次の(a)及び(b)の問に答えよ。
(a)貯湯タンク内の水の加熱に必要な熱エネルギー Qの値[MJ]として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(b)電気給湯器としてCOP (成績係数)が4.0のヒートポンプユニットを用いた。この加熱に要した時間は6時間であった。ヒートポンプユニットの消費電力Pの値[kW]として,最も近いものを次の(1)~(5)のうちから一つ選べ。ただし,ヒートポンプ式電気給湯器の貯湯タンク,ヒートポンプユニット,配管などの加熱に必要な熱エネルギーは無視し,それらからの熱損失もないものとする。また,ヒートポンプユニットの消費電力及びCOPは,いずれも加熱の開始から終了まで一定とする。
解説・コメント
(a)
加熱に必要なエネルギーは比熱容量×質量×温度差であり、質量は密度×体積で計算できる。
熱エネルギーQ=4.18×10\(^3\) ×0.37×1×10\(^3\)×(85-35)≒100.5[MJ](b)
熱エネルギーQはCOP×消費エネルギー×時間で表される。
消費エネルギーをP[kW]とすると、
100.5×10\(^6\)=P×4×P×6×3600
P≒1.16[kW]https://ja.mondder.com/fq?id=1780🔗
問題文正答率:33.33%
問18 論理関数について,次の(a)及び(b)の問に答えよ。
(a)論理式\(X・Y・Z + X・\overline{Y}・\overline{Z} + \overline{X}・Y・Z + X・\overline{Y}・Z\) を積和形式で簡単化したものとして,正しいものを次の(1)~(5)のうちから一つ選べ。
(b)論理式\((X+Y+Z)・(X+Y+\overline{Z})・(X+\overline{Y}+Z)\)を和積形式で簡単化したものとして,正しいものを次の(1)~(5)のうちから一つ選べ。
解説・コメント
(a)
4項を並び替えて、前の2項と後ろの2項をそれぞれ吸収の定理を利用してまとめる。
X・Y・Z + \overline{X}・Y・Z + X・\overline{Y}・\overline{Z} + X・\overline{Y}・Z\→Y・Z (X + \overline{X}) + X・\overline{Y}(\overline{Z} +Z)
それぞれ()内は1であるため、
→Y・Z + X・\overline{Y}
(b)
論理式の出力をWとして、それぞれの数値を入力して試行錯誤を行う。
・X=1,Y=0,Z=0のときW=1 → (4)はW=0であるため、(4)は誤
・X=0,Y=1,Z=0のときW=0 → (3)はW=1であるため、(3)は誤
・X=0,Y=0,Z=1のときW=0 → (2)はW=1であるため、(2)は誤
・X=1,Y=0,Z=1のときW=1 → (5)はW=0であるため、(5)は誤
https://ja.mondder.com/fq?id=1781🔗
0
解説・コメント
直流機ではEは回転速度Nと界磁磁束φに比例する。
本問では、φは永久磁束であるため一定であり、EはNにのみ比例するため、E=kNと表すことができる。
E=kN
100=1000k → k=0.1
電源電圧が100Vのとき、E'=100-1×20=80
80=0.1×N' → N'=800[min\(^{-1}\)]