確率と統計 ITパスポート対策テクノロジ系基礎理論編③
8 views
2023-10-192023-10-19
確率の基本
場合の数
ある事柄について起こりうるパターンが何通りあるかを数えたものを場合の数といいます。
順列
異なるn個の中からr個を取り出して順番に並べた場合の総パターン数は以下のようになります。
\[ _nP_r = n×(n-1)×(n-2)×(n-3)…(n-r+1)\]例えば、6枚のカードから3枚をとって並べるなら、
\[ _6P_3 = 6×5×4=120\]となります。
組合せ
並び順は考えずに異なるn個の中からr個を取り出す場合の、総パターン数は以下のようになります。
\[ _nC_r = \frac{_nP_r}{r!}\]例えば、6枚のカードから3枚を取り出すなら、
\[ _6C_3 = \frac{6×5×4}{3×2×1} = 20\]となります。
確率
確率とは、事象の起こる可能性の度合いのことで、一般には
\[ P(A) = \frac{ある事象が起こる場合の数}{起こり得る全ての場合の数}\]で表されます。
データの代表値
統計ではデータを代表する値として以下のようなものが使用されます。
平均値
データを足し合わせたものをデータ数で割った値が平均です。
\[平均 = \frac{データの総和}{全データ数} \]例えば、8、10、6、9、5 という5個のデータがあった場合、平均は、
\[平均 = \frac{8+10+6+9+5}{5}=7.6 \]となります。
中央値(メジアン)
データを昇順または降順に並べ替えた時に真ん中に位置する値が中央値です。データの数が偶数の場合は、ちょうど中央に来る値がないので2つの平均値を中央値とします。
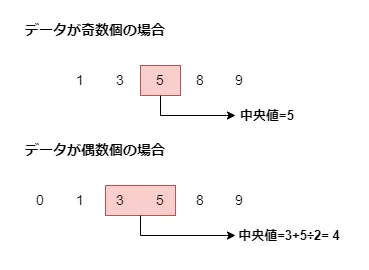
最頻値(モード)
データの中で出現回数の最も多い値が最頻値です。
例えば、1、3、6、3、5、1、4、1というデータの場合、3回でてくる「1」が最頻値ということになります。
期待値
期待値は平たく言えば確率が絡む際の平均値の様なもので、離散型の場合は、
\[期待値= \sum_{i=1}^{n}xipi \]と定義されます。
例えば、投資を行った結果1年後に、20%の確率で100万円が、30%の確率で80万円が、50%の確率で60万円が得られるとすると、期待値は、
\[100万×0.2 + 80万円×0.3 + 60万円×0.5 = 74万円\]となります。
データのばらつき
データのばらつきを表す値には以下のようなものがあります。
分散
個々のデータから平均値を引いて二乗にたものを足し合わせてからテータ数で割った値が分散で、データがどの程度まとまっているか(平均に近い値で構成されているか)をみることができます。
\[分散= \frac{1}{n}\sum_{i=1}^{n}(x-\bar{x})^2 \]例えば、10、30、40、20、15というデータがあるとします。このデータの平均値は(10+30+40+20+15)÷5=23ですので、分散は、
\[ ( (10-23)^2 + (30-23)^2 + (40-23)^2 +(20-23)^2 + (15-23)^2 ) ÷ 5 = 116 \]となります。
標準偏差
標準偏差は、分散の平方根を求めた値です。
\[ 標準偏差 = \sqrt{分散} \]上の分散値ですと、
\[ \sqrt{116} = 10.77032… \]となります。
偏差値
偏差値は、あるデータが全体の中でどの位置あるのかを分かりやすく表した値で、以下の式で定義されます。
\[ 偏差値 = \frac{(あるデータ - 平均値)}{標準偏差}×10+50 \]例えば、自分の得点が72点、平均が60点、標準偏差が8だったとすると、
\[ \frac{(75 - 60)}{8}×10+50 = 68.75 \]となります。
正規分布を仮定すれば、平均である偏差値50からの±10区間に全体の約68.3%が収まることになります。
その他応用数学
グラフ理論
グラフ理論は、点(ノード)と辺(エッジ)で表される図形に関する数学的な理論で、交通網や電気回路、Webサイトのリンク構造の分析などに応用されています。
グラフには、辺が方向を持つ有向グラフと持たない無向グラフがあります。
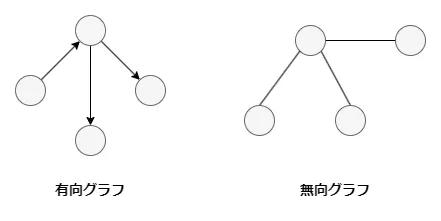
待ち行列理論
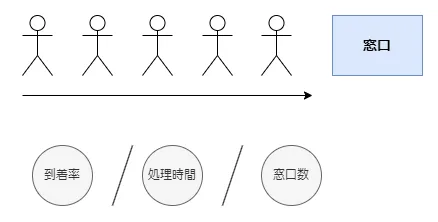
レジで会計をする顧客の列など順番待ちとその処理をモデル化したもので、待ち時間の平均などを求めるために利用されます。よく知られたモデルに到着がポアソン分布、処理時間が指数分布に従い窓口が1つなM/M/1モデルがあります。
確認問題(過去問)
ITパスポート試験令和元年問72
人の候補者の中から兼任も許す方法で委員長と書記を1名ずつ選ぶ場合,3人の中から委員長1名の選び方が3通りで,3人の中から書記1名の選び方が3通りであるので, 委員長と書記の選び方は全部で9通りある。5人の候補者の中から兼任も許す方法で 委員長と書記を1名ずつ選ぶ場合,選び方は何通りあるか。
ITパスポート試験平成28年春問98
それぞれが独立に点灯/消灯の操作ができる5個のランプが並んでいる。2個以上のランプが点灯しているパターンは何通りあるか。 ここで,全てが点灯しているパターンは1通り,いずれか1個が点灯しているパターンは5通りと数えるものとする。
ITパスポート試験令和4年問59
次のデータの平均値と中央値の組合せはどれか。
[データ]10, 20, 20, 20, 40, 50, 100, 440, 2000
基本情報技術者試験令和元年秋問5
平均が 60,標準偏差が 10 の正規分布を表すグラフはどれか。
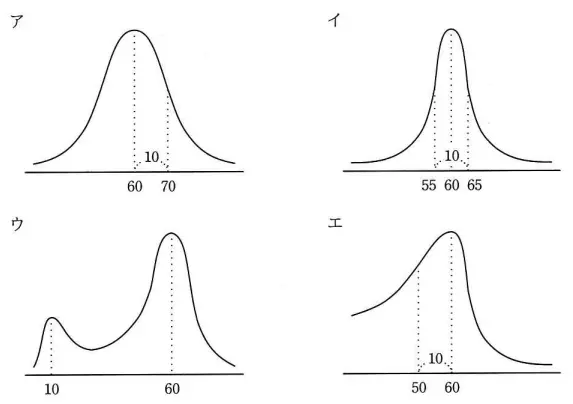
ITパスポート試験令和5年問77
受験者10,000人の4教科の試験結果は表のとおりであり,いずれの教科の得点分布も正規分布に従っていたとする。 ある受験者の4教科の得点が全て71点であったときこの受験者が最も高い偏差値を得た教科はどれか。
| 平均点 | 標準偏差 | |
|---|---|---|
| 国語 | 62 | 5 |
| 社会 | 55 | 9 |
| 数学 | 58 | 6 |
| 理科 | 60 | 7 |
これだけで受かるITパスポート
https://ja.mondder.com
